In this type of right triangle, the sides corresponding to the angles 30°60°90° follow a ratio of 1√ 3 2 Thus, in this type of triangle, if the length of one side and the side's corresponding angle is known, the length of the other sides can be determined using the above ratio Since it's a right triangle, we know that one of the angles is a right angle, or 90º, meaning the other must by 60º This is a triangle, and the sides are in a ratio of x x 3 2 x, with x being the length of the shortest side, in this case 7 The other sides must be 7 ⋅ 3 and 7 ⋅ 2, or 7 3 and 14A 30 ° − 60 ° − 90 ° triangle is commonly encountered right triangle whose sides are in the proportion 1 3 2 The measures of the sides are x , x 3 , and 2 x In a 30 ° − 60 ° − 90 ° triangle, the length of the hypotenuse is twice the length of the shorter leg, and the length of the longer leg is 3 times the length of the shorter leg

Special Right Triangles 30 60 90 And 45 45 90 Triangles Youtube
Sides of a 30 60 90 right triangle
Sides of a 30 60 90 right triangle- A triangle is a special right triangle (a right triangle being any triangle that contains a 90 degree angle) that always has degree angles of 30 degrees, 60 degrees, and 90 degrees Because it is a special triangle, it also has side length values which are always in a consistent relationship with one anotherThe reason these triangles are considered special is because of the ratios of their sides they are always the same!




The Complete Guide To The 30 60 90 Triangle
A triangle is a right triangle with angles 30^@, 60^@, and 90^@ and which has the useful property of having easily calculable side lengths without use of trigonometric functions A triangle is a special right triangle, so named for the measure of its angles Its side lengths may be derived in the following mannerThe hypotenuse is the longest side in a right triangle, which is different from the long leg The long leg is the leg opposite the 60degree angle Two of the most common right triangles are and the degree triangles All triangles have sides 30 60 90 Triangle Working Methodology To resolve our right triangle as a 30 60 90, we have to establish very first that the three angles of the triangular are 30, 60, and 90 Resolve for the side sizes;
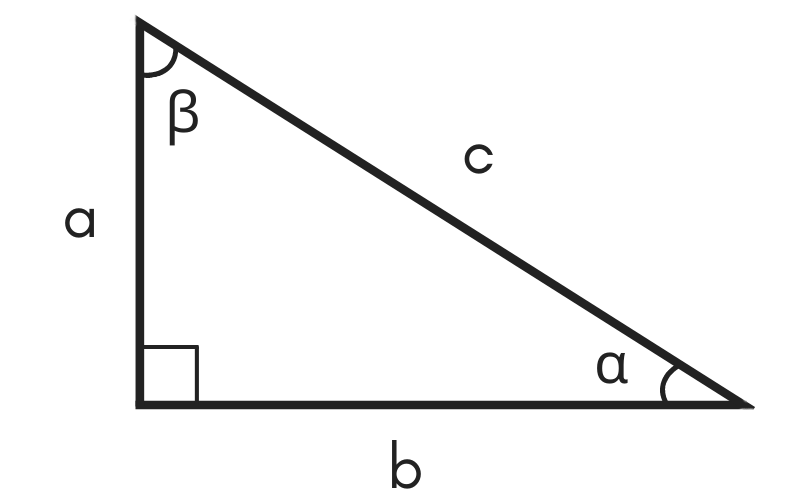
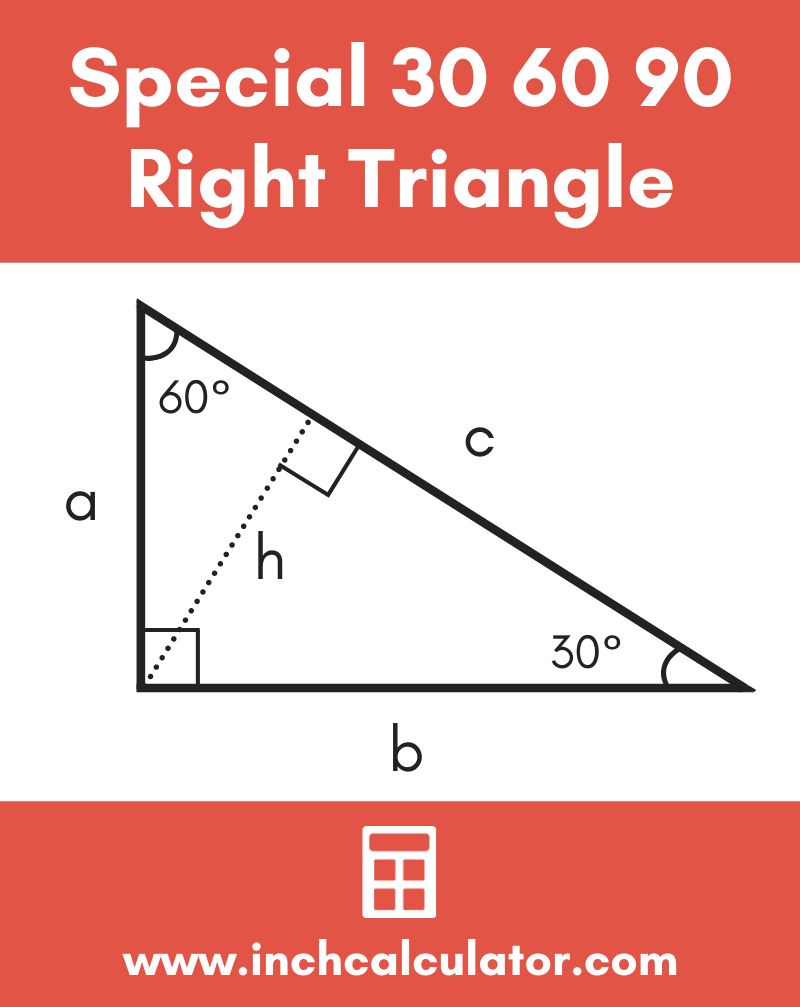
Sides of right triangle 30 60 90 The basic triangle ratio is Side opposite the 30° angle x Side opposite the 60° angle x * √3 Side opposite the 90° angle 2x All degree triangles have sides with the same basic ratio Two of the most common right triangles are and degree triangles If you look at the 30–60–90degree triangle inSpecial Triangles Isosceles and Calculator This calculator performs either of 2 items 1) If you are given a right triangle, the calculator will determine the missing 2 sides Enter the side that is known After this, press Solve Triangle 2) In addition, the calculator will allow you to same as Step 1 with a right triangleSides Of Right Triangle 30 60 90 Using the technique in the model above, find the missing side in this 30°60°90° right triangle Short = 5, hypotenuse = 10 Long = 5 sqrt 3 Click an item in the list or group of pictures at the bottom of the problem and, holding the button down, drag it into the correct position in the answer box
A is a scalene triangle and each side has a different measure Since it's a right triangle, the sides touching the right angle are called the legs of the triangle, it has a long leg and a short leg, and the hypotenuse is the side across fromSince this is a right triangle, we know that the sides exist in the proportion 1 √3 3 2 The shortest side, 1, is opposite the 30 degree angle Since side X is opposite the 60 degree angle, we know that it is equal to 1∗ √3 1 ∗ 3, or about 173See also Side /angle relationships of a triangle In the figure above, as you drag the vertices of the triangle to resize it, the angles remain fixed and the sides remain in this ratio Corollary If any triangle has its sides in the ratio 1 2 √3, then it is a triangle



1




Special Right Triangles 30 60 90 And 45 45 90 Triangles Youtube
Now in every 30°60°90° triangle, the sides are in the ratio 1 2 , as shown on the right Whenever we know the ratios of the sides, we can solve the triangle by the method of similar figures And so in triangle ABC, the side corresponding to 2 has been multipliedby 5 Therefore every side will be multiplied by 5I am assuming when you say a 30–60–90 triangle you mean a right triangle with acute angles of 30 degrees and 60 degrees, a 30°60°90° triangle A 30°60°90° triangle, can be constructed by dividing an equilateral triangle in half, because of this fact and the Pythagorean theorem the sides lengths are in a ratio of 1, √3, and 2A triangle is a right triangle with angle measures of 30º, 60º, and 90º (the right angle) Because the angles are always in that ratio, the sides are




30 60 90 Special Right Triangles Youtube




The Complete Guide To The 30 60 90 Triangle
This is a triangle with one side length given Let's find the length of the other two sides, a and b Since the side you are given, 8, is across from the 30Special right triangles hold many applications in both geometry and trigonometry In this lesson you will learn the general formula for the ratios, and how to find missing sides of any 30 60 90 right triangleThe triangle is one example of a special right triangle It is right triangle whose angles are 30°, 60° and 90° The lengths of the sides of a triangle are in the ratio of 1√32 The following diagram shows a triangle and the ratio of the sides Scroll down the page for more examples and solutions on how to use the triangle



30 60 90 Special Right Triangle Calculator Inch Calculator




In A 30 60 90 Right Triangle The Side Opposite The 30 Degree Angle Is Brainly Com
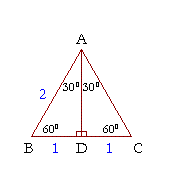
Triangle in trigonometry In the study of trigonometry, the triangle is considered a special triangleKnowing the ratio of the sides of a triangle allows us to find the exact values of the three trigonometric functions sine, cosine, and tangent for the angles 30° and 60° For example, sin(30°), read as the sine of 30 degrees, is the ratio of the side A $$ is one of the must basic triangles known in geometry and you are expected to understand and grasp it very easily In an equilateral triangle, angles are equal As they add to $180$ then angles are are all $\frac {180}{3} = 60$ And as the sides are equal all sides are equal (see image) So that is a $$ triangleA minimum of 1 side size has to be already understood If we know that we are collaborating with an appropriate triangle, we understand that



The Easy Guide To The 30 60 90 Triangle



30 60 90 Right Triangle Side Ratios Expii
30 60 90 Triangle Example Problem Video Khan Academy 30 60 90 Triangle Formula For Sides, A 30 60 90 Triangle Ppt Side Relationships In Special Right Triangles Exact ValuesAs one angle is 90, so this triangle is always a right triangle As explained above that it is a special triangle so it has special values of lengths and angles The basic triangle sides ratio is The side opposite the 30° angle x The side opposite👉 Learn about the special right triangles A special right triangle is a right triangle having angles of 30, 60, 90, or 45, 45, 90 Knowledge of the ratio o




How To Work With 30 60 90 Degree Triangles Education Is Around




30 60 90 Triangle Definition Theorem Formula Examples
Does your geometry homework have you stumped about finding the sides of a right triangle? A right triangle is a special type of right triangle 30 60 90 triangle's three angles measure 30 degrees, 60 degrees, and 90 degrees The triangle is significant because the sides exist in an easytoremember ratio 1√(3/2)30°60°90° triangle is actually the equilateral triangle cut along the altitude The relationship between sides can be established by choosing hypotenuse as 2a The short leg (a) is opposite to 30° angle and it is half the length of the hypotenus




30 60 90 Triangle Theorem Ratio Formula Video



30 60 90 Special Right Triangle Calculator Inch Calculator
A triangle is a special right triangle whose angles are 30º, 60º, and 90º The triangle is special because its side lengths are always in the ratio of 1 √32 Any triangle of the form can be solved without applying longstep methods such as the Pythagorean Theorem and trigonometric functionsTriangles are classified as "special right triangles" They are special because of special relationships among the triangle legs that allow one to easily arrive at the length of the sides with exact answers instead of decimal approximations when using trig functionsA triangle is a special right triangle (a right triangle being any triangle that contains a 90 degree angle) that always has degree angles of 30 degrees, 60 degrees, and 90 degrees Because it is a special triangle, it also has side length values which are always in a consistent relationship with one another



Special Right Triangles Exploration 30 60 90 And 45 45 90 Full Package
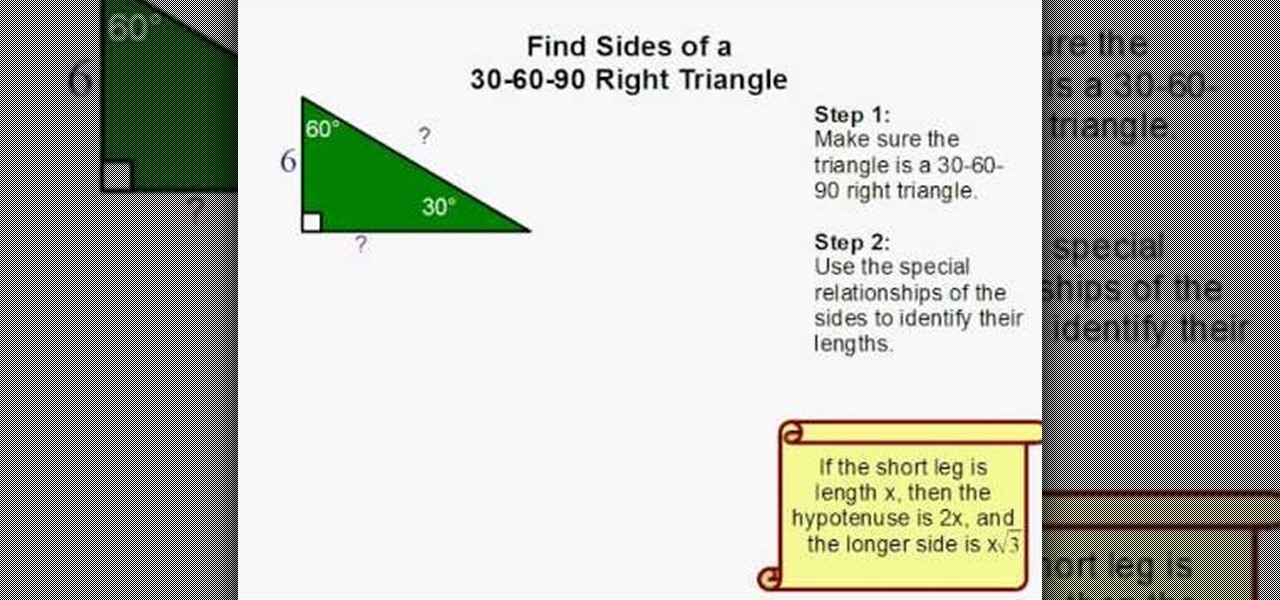



How To Find The Sides Of A 30 60 90 Right Triangle Math Wonderhowto
Using what we know about triangles to solve what at first seems to be a challenging problem Created by Sal Khan Special right triangles Special right triangles proof (part 1) Special right triangles proof (part 2) Practice Special right triangles triangle example problem This is the currently selected item 30 60 90 Triangle Ratio A triangle is a special right triangle (a right triangle being any triangle that contains a 90 degree angle) that always has degree angles of 30 degrees, 60 degrees, and 90 degrees Because it is a special triangle, it also has side length values which are always in a consistent relationship with one another What Is a Triangle?




How To Use The Special Right Triangle 30 60 90 Studypug



Triangle 30 60 90 Clipart Etc
30 60 90 triangle sides If we know the shorter leg length a, we can find out that b = a√3 c = 2a If the longer leg length b is the one parameter given, then a = b√3/3 c = 2b√3/3 For hypotenuse c known, the legs formulas look as follows a = c/2 b = c√3/2 Or simply type your given values and the 30 60 90 triangle calculator will do the rest!Special Right Triangles Angle based Side based A special right triangle is a right triangle with some regular feature that makes calculations on the triangle easier, or for which simple formulas exist Angle based right triangle , (Angles that form a simple ratio) Side based right triangle 345 (The lengths of the sides form a whole number ratio), approx anglesTriangle Ratio A degree triangle is a special right triangle, so it's side lengths are always consistent with each other The ratio of the sides follow the triangle ratio 1 2 √3 1 2 3 Short side (opposite the 30 30 degree angle) = x x




Day 1 Hw Special Right Triangles 45 45 90 30 60 90 Youtube Trigonometry Worksheets Right Triangle Triangle Worksheet




30 60 90 Special Right Triangle Calculator Inch Calculator
A triangle is a right triangle with angle measures of 30º, 60º, and 90º (the right angle) Because the angles are always in that ratio, the sides are👉 Learn about the special right triangles A special right triangle is a right triangle having angles of 30, 60, 90, or 45, 45, 90 Knowledge of the ratio oHave no fear, in this excellent video, Davitily from Math Problem Generator explains the process step by step using easy to follow examples The video covers common examples and tricky snags that you are likely to encounter on your next math class exam
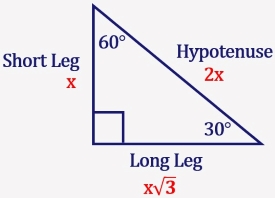



Find The Side Lengths Of A Special Right Triangle 30 60 90 Mathondemand Com




The Complete Guide To The 30 60 90 Triangle
Đang xem Geometry triangle practice The side opposite the 30° angle is always the smallest, because 30 degrees is the smallest angle The side opposite the 60° angle will be the middle length, because 60 degrees is the midsized degree angle in this triangleAlthough all right triangles have special features – trigonometric functions and the Pythagorean theoremThe most frequently studied right triangles, the special right triangles, are the 30, 60, 90 Triangles followed by the 45, 45, 90 triangles The key characteristic of a right triangle is that its angles have measures of 30 degrees (π/6 rads), 60 degrees (π/3 rads) and 90 degrees (π/2 rads) The sides of a right triangle lie in the ratio 1√32 The side lengths and angle measurements of a right triangle Credit Public Domain




30 60 90 Triangle Theorem Ratio Formula Video




A Quick Guide To The 30 60 90 Degree Triangle Dummies
Special Triangle Relationships Triangles A triangle is a right triangle whose internal angles are 30, 60 and 90 degrees The three sides of a triangle have the following characteristics All three sides have different lengths The shorter leg, b, is half the length of the hypotenuse, c That is, b=c/2To fully solve our right triangle as a 30 60 90, we have to first determine that the 3 angles of the triangle are 30, 60, and 90 To solve for the side lengths, a minimum of 1 side length must already be known If we know that we are working with a right triangle, we know that one of the angles is 90Right triangle calculator, 30 60 90 formula, 45 triangle, special area, unit circle calculator




Act Set 6 Special Right Triangle Rules Flashcards Quizlet



Solution I Dont Know How Do 30 60 90 Triangles That Already Have One Side And Also 45 45 90 Triangles And Sin 1 And All That Please Help
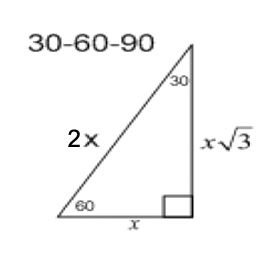



Special Right Triangles Geometry Quizizz




30 60 90 Right Triangles Solutions Examples Videos



1




Special Right Triangles Fun Group Activity 30 60 90 And 45 45 90




Solved 1 For A 30 60 90 Triangle It Is Known That The Chegg Com




30 60 90 45 45 90 Special Right Triangles Free Printable Math Worksheets Teaching Geometry Printable Math Worksheets
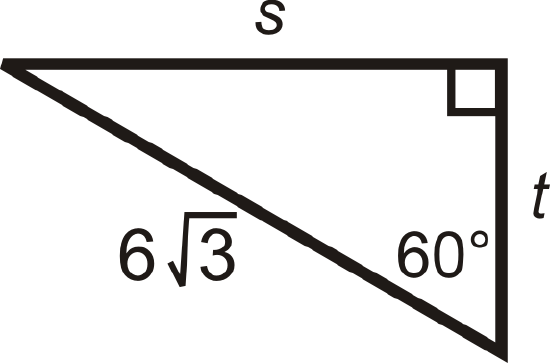



4 43 30 60 90 Right Triangles K12 Libretexts




30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com



30 60 90 Right Triangles Consider The Following
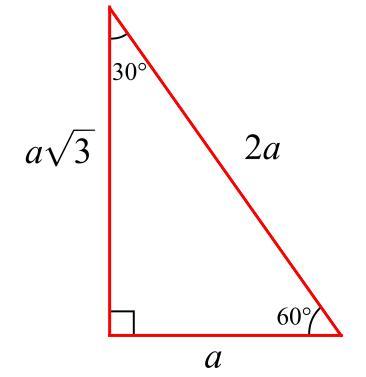



Which Of The Following Are True Statements About A 30 60 90 Triangle Check All That Apply



The Easy Guide To The 30 60 90 Triangle



The Easy Guide To The 30 60 90 Triangle



The Easy Guide To The 30 60 90 Triangle



45 45 90 And 30 60 90 Triangles Zona Land Education




30 60 90 Triangle Explanation Examples




30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com




30 60 90 Triangle Explanation Examples
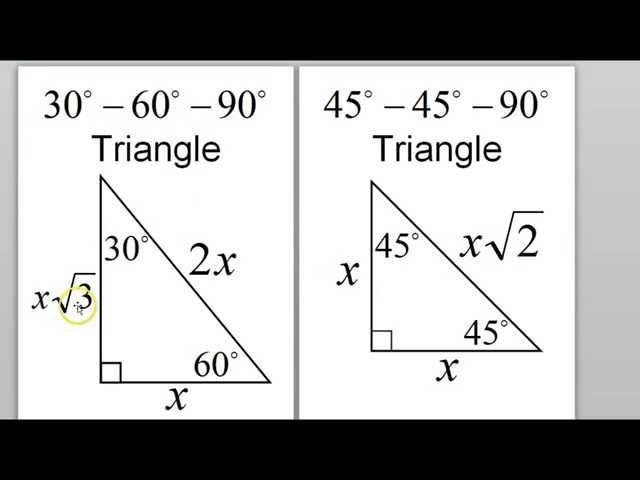



Special Right Triangles 30 60 90 Worksheet Jobs Ecityworks
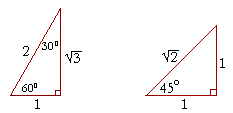



The 30 60 90 Triangle Topics In Trigonometry




Relationships Of Sides In 30 60 90 Right Triangles Ck 12 Foundation




30 60 90 Triangle Theorem Ratio Formula Video




The 30 60 90 Triangle Topics In Trigonometry




Relationships Of Sides In 30 60 90 Right Triangles Ck 12 Foundation




30 60 90 Triangles



Special Right Triangle 30 60 90 Mathbitsnotebook Geo Ccss Math



Is A 3 4 5 Triangle Also A 30 60 90 Triangle Quora




30 60 90 Right Triangles Ck 12 Foundation




Special Right Triangles 30 60 90 And 45 45 90 Triangles Matter Of Math
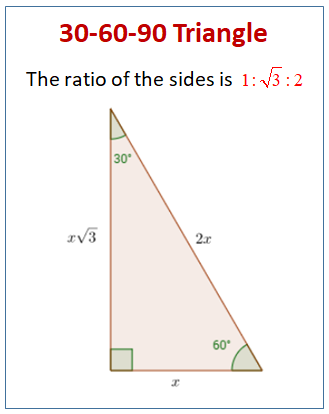



30 60 90 Special Right Triangles Videos Worksheets Examples Solutions
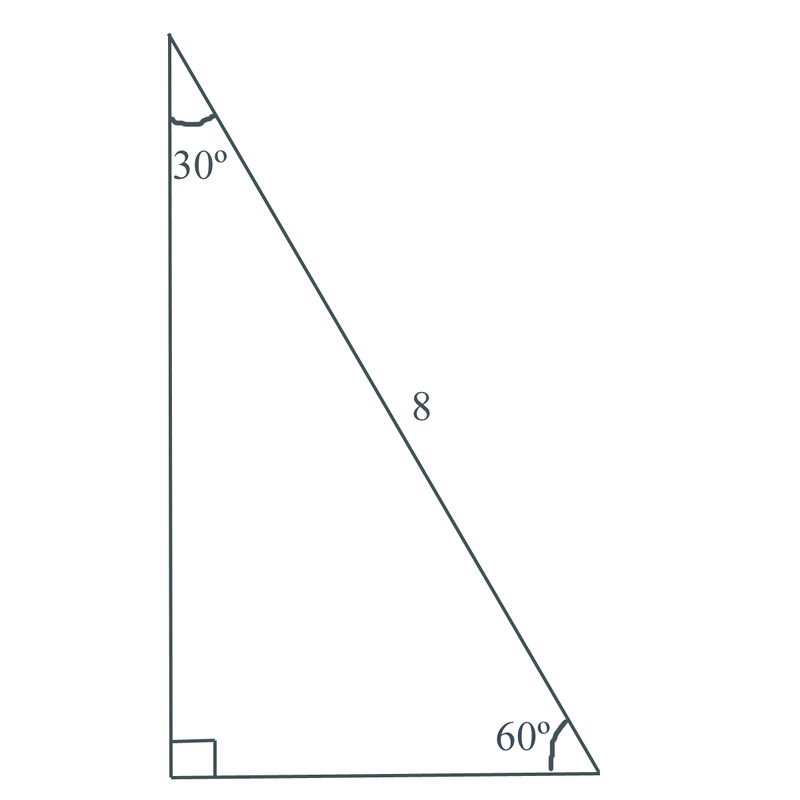



Relationships Of Sides In 30 60 90 Right Triangles Ck 12 Foundation
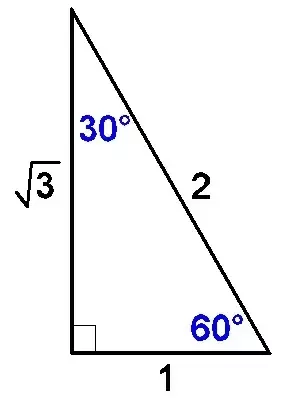



30 60 90 Right Triangle How Do I Solve If The Long Leg Is 10 Socratic
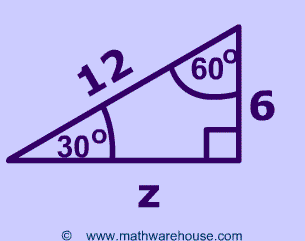



Special Right Triangles Formulas 30 60 90 And 45 45 90 Special Right Triangles Examples Pictures And Practice Problems



Trigonometry




Solved Trigonometry Prerequisite Special Right Triangles Chegg Com



Solve A 30 60 90 Triangle With Gradea




30 60 90 Triangle Formulas Rules And Sides Science Trends
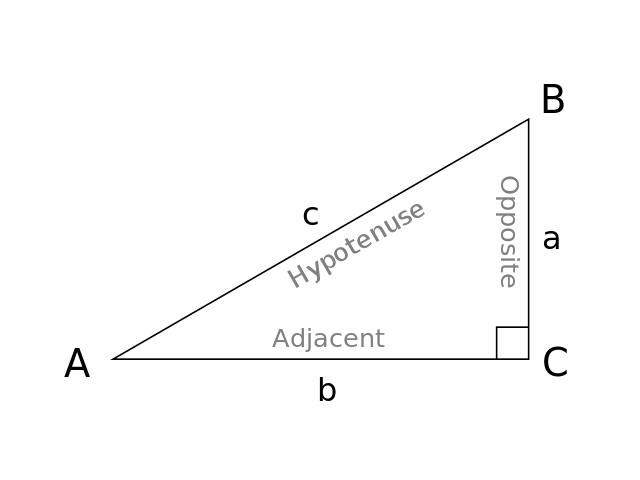



30 60 90 Triangle Formulas Rules And Sides Science Trends




30 60 90 Right Triangles Free Math Help
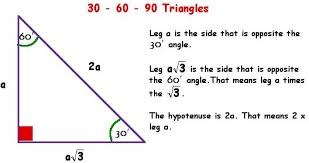



30 60 90 Right Triangle Theorem By Stephanie Joaquin Infographic
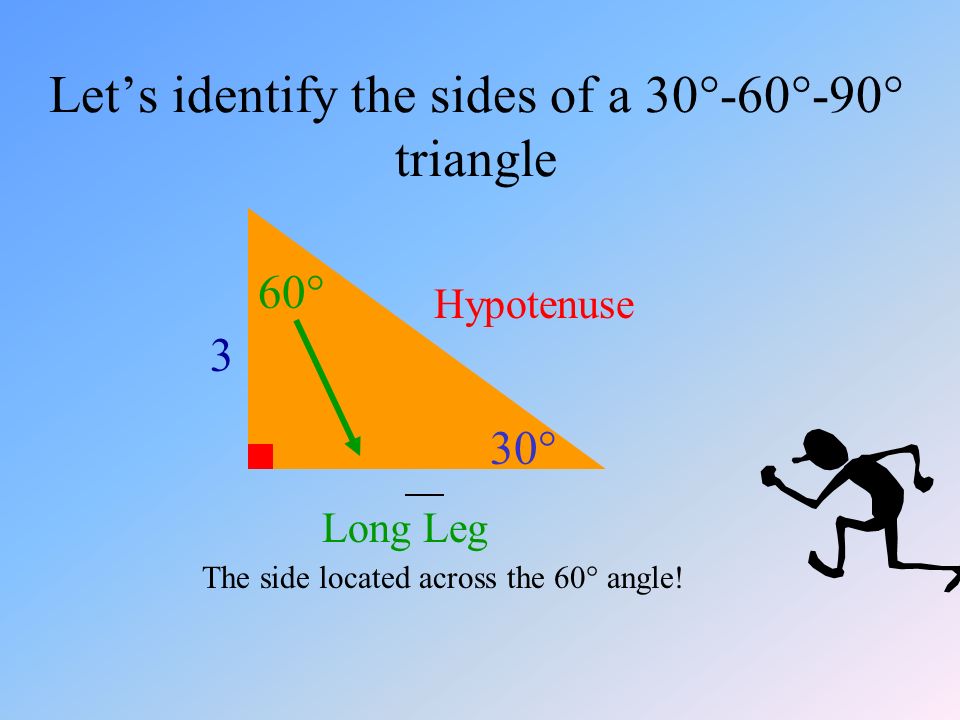



30 60 90 Triangles And You Remember The Pythagorean Theorem The Sum Of The Square Of The Legs Is Equal To The Square Of The Hypotenuse A Ppt Download




30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com



1




Relationships Of Sides In 30 60 90 Right Triangles Ck 12 Foundation




30 60 90 Right Triangle Side Ratios Expii
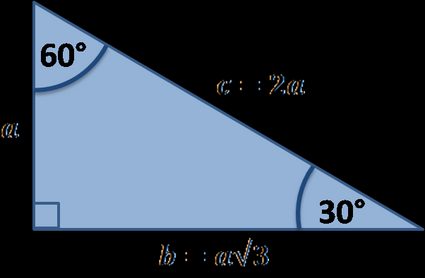



30 60 90 Triangle Calculator Formula Rules




30 60 90 Triangle Definition Theorem Formula Examples
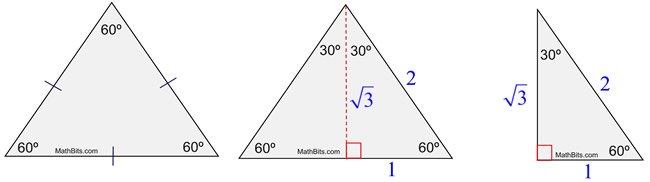



Special Right Triangle 30 60 90 Mathbitsnotebook Geo Ccss Math
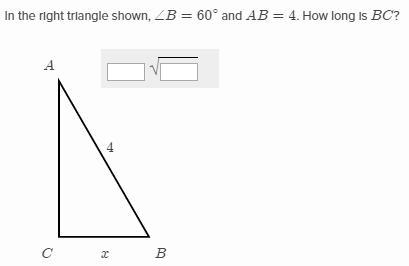



Special Right Triangles Khan Academy Wiki Fandom




30 60 90 Triangle Theorem Proof Don T Memorise Youtube




A Quick Guide To The 30 60 90 Degree Triangle Dummies
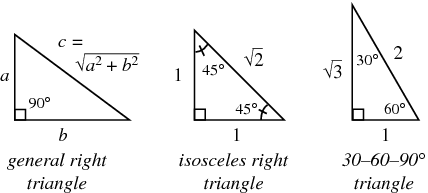



Right Triangle From Wolfram Mathworld
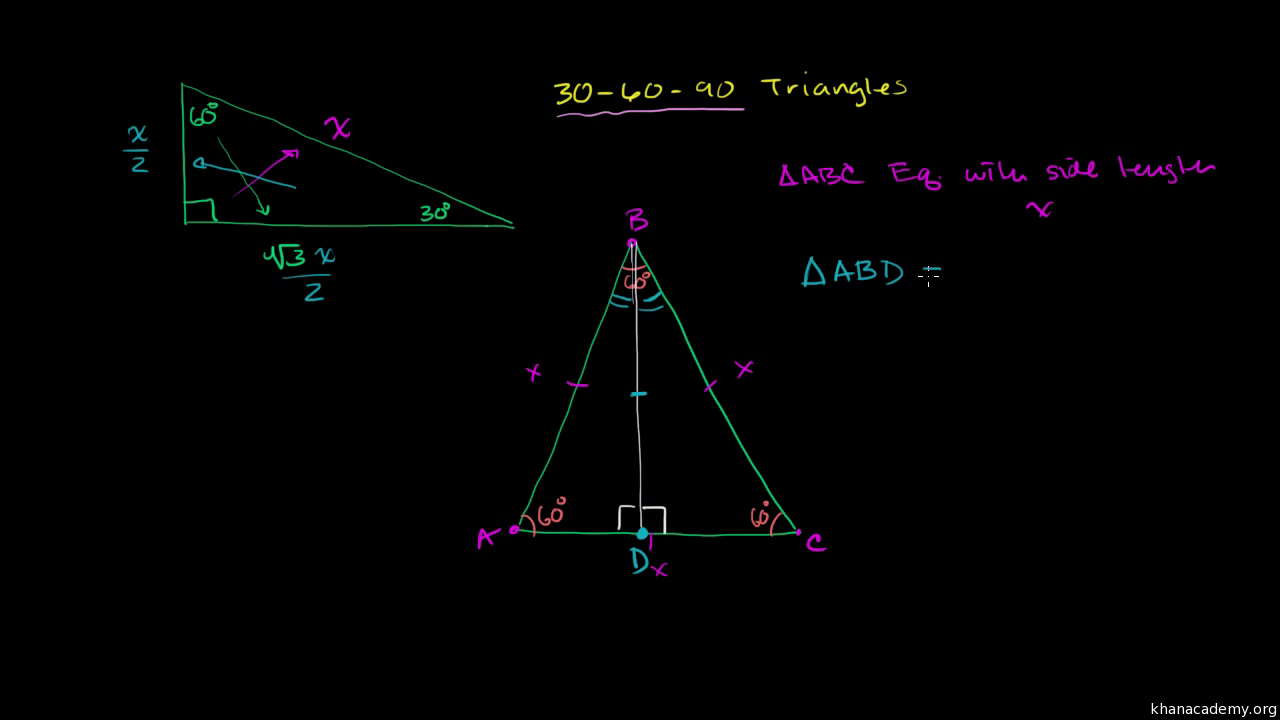



Special Right Triangles Proof Part 1 Video Khan Academy




Velocity
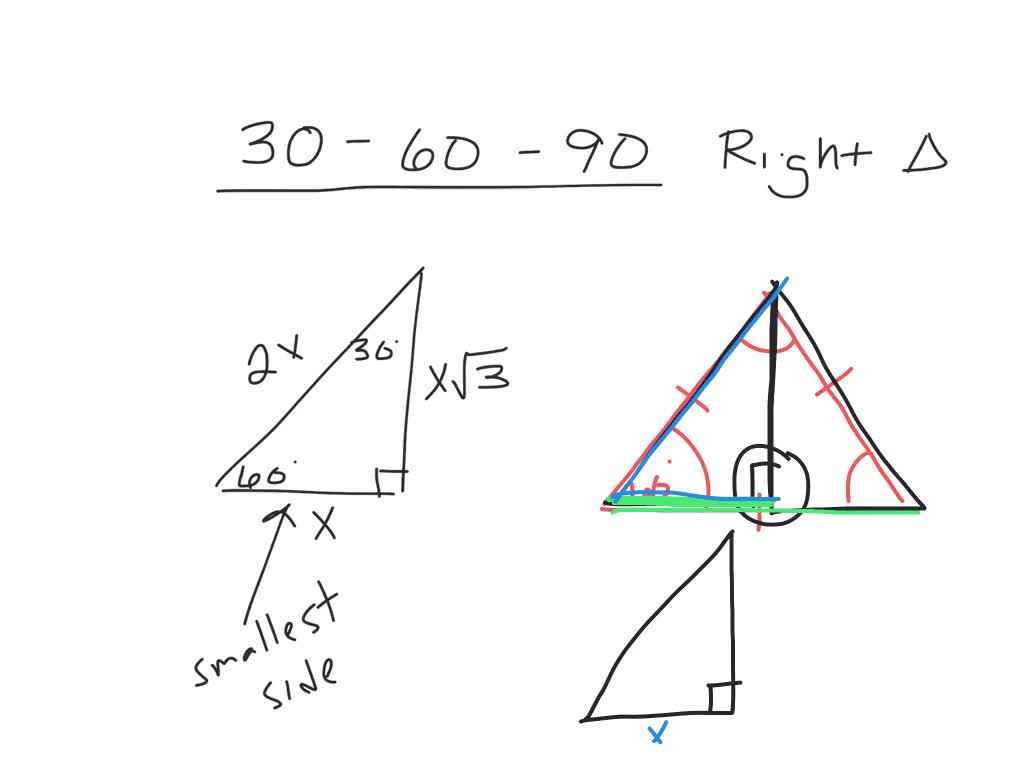



30 60 90 Right Triangles Numerade




30 60 90 Triangle Calculator Formula Rules
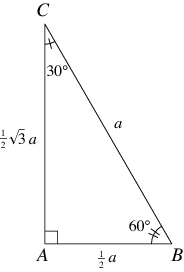



30 60 90 Triangle From Wolfram Mathworld
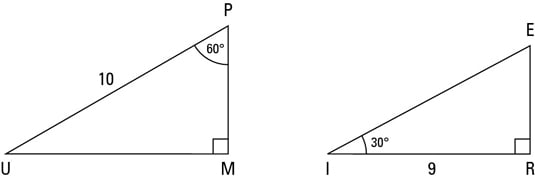



Identifying The 30 60 90 Degree Triangle Dummies




Special Right Triangles Fully Explained W 19 Examples




Special Right Triangles Video Lessons Examples And Solutions




Solved Special Right Triangles 30 Degree 60 Degree 90 Chegg Com




Triangles And Lines Special Right Triangles There Are Two Special Right Triangles 30 60 90 Degree Right Triangle 45 45 90 Degree Right Triangle Ppt Download



Lesson 1 Special Right Triangles 30 60 90 Frys Nc Math 2 Honors S2



30 60 90 Triangle Rules



If A Right Angled Triangle 30 60 90 Hypotenuse Is 10 Cm Then What Is The Length Of The Side Opposite To 60 Angle Quora
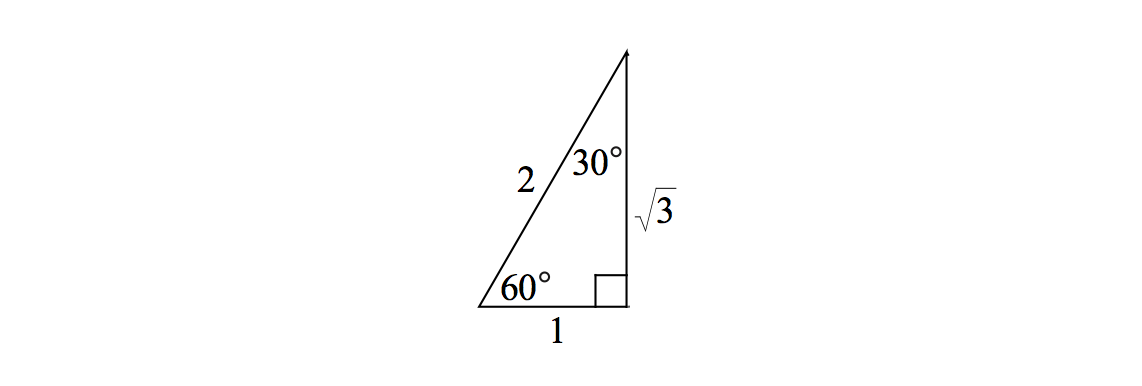



Lengths In Right Triangles Brilliant Math Science Wiki




5 8 Special Right Triangles




30 60 90 Triangle Theorem Ratio Formula Video



1
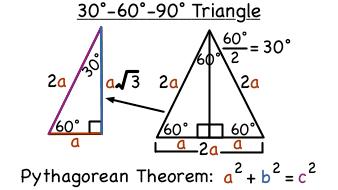



What Is A 30 60 90 Degree Triangle Virtual Nerd




30 60 90 Triangles Hd Youtube




30 60 90 Triangle Example Problem Video Khan Academy
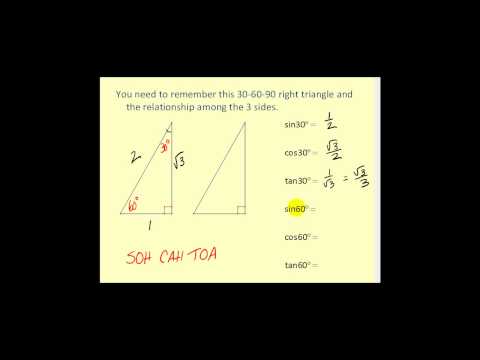



4 43 30 60 90 Right Triangles K12 Libretexts
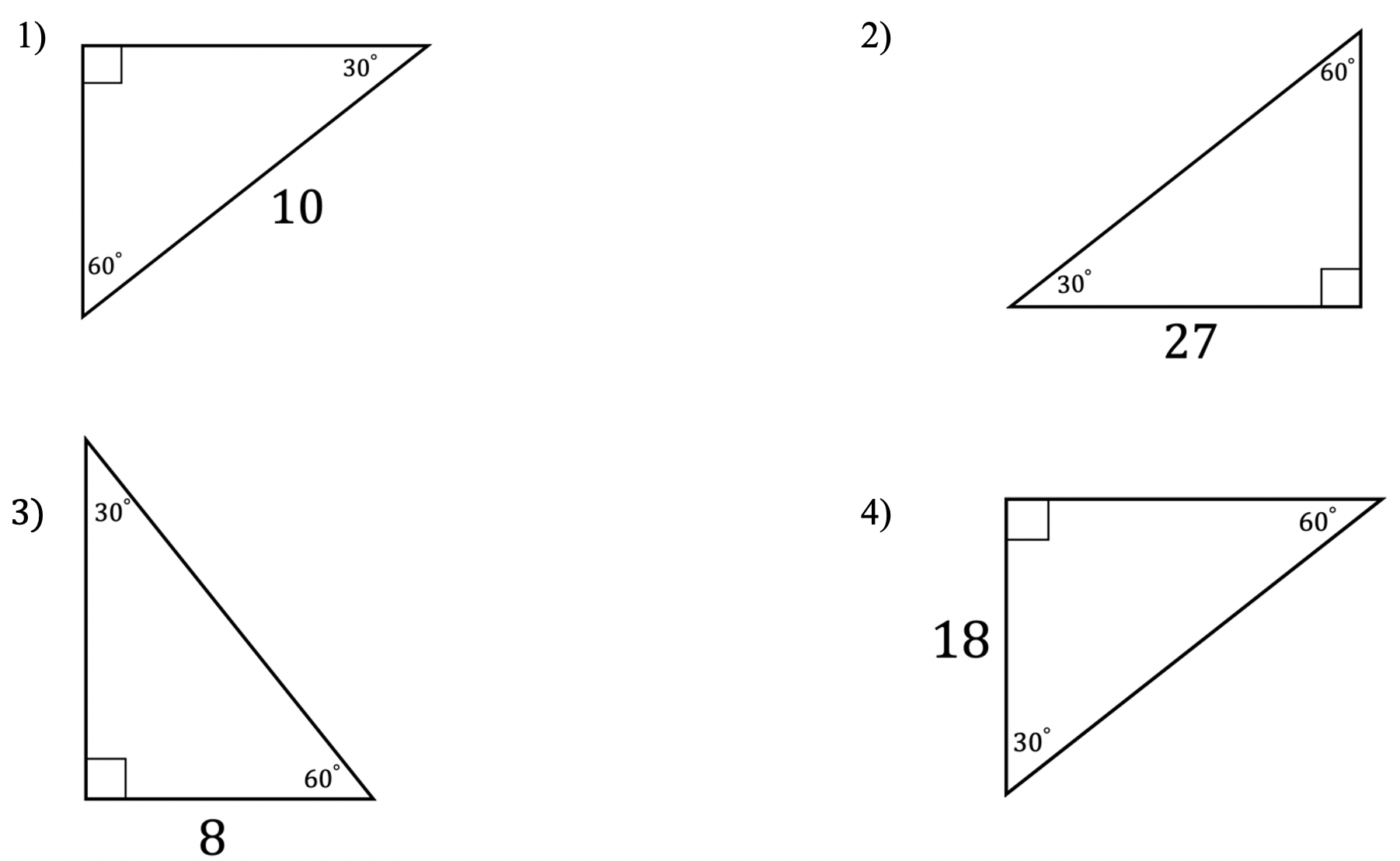



30 60 90 Special Triangles Geometry Mathsux 2




30 60 90 Triangle Theorem Ratio Formula Video



30 60 90 Right Triangles And Algebra Examples Beacon Learning




30 60 90 Triangle Calculator Formula Rules




Special Right Triangle Wikipedia




Use 45 45 90 Amp 30 60 90 Special Right Triangles To Solve Find The Missing Sir Length Leave You Brainly Com



The Easy Guide To The 30 60 90 Triangle




Conquering Right Triangles The Pythagorean Theorem On Act Math Part 1 Magoosh Blog High School



0 件のコメント:
コメントを投稿